순차 탐색(Linear Search) 알고리즘과 시간 복잡도 분석의 핵심요소
Programming/Data Structure 2012. 12. 20. 01:31 |순차 탐색 알고리즘으로 시간 복잡도 계산
순서 탐색 알고리즘
- 맨 앞에서부터 순서대로 탐색을 진행하는 알고리즘이기에 순차 탐색이라는 이름이 붙어있다.
for(i=0; i<len; i++)
{
if(ar[i] == target)
return i;
}
위의 코드를 토대로 시간 복잡도를 분석해서 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구해보자.
일단, 이 알고리즘에서 사용된 연산자는 <, ++, == 이렇게 세 개이다. 이 연산자들이 얼마나 많이 수행이되는지를 분석하면 되는데...
이 질문에 답을 하고 분석을 진행해야 한다.
"어떠한 연산을 적게 수행하는 탐색 알고리즘이 좋은 탐색 알고리즘인가?"
탐색 알고리즘에서 값의 동등을 비교하는 == 연산을 적게 수행하는 탐색 알고리즘이 좋은 탐색 알고리즘이다.
즉, 탐색 알고리즘에서의 핵심은 동등비교를 하는 비교연산에 있다. 비교연산의 수행횟수가 줄어들면 < 연산과 ++ 연산의 수행횟수도 줄어들고, 비교연산의 수행횟수가 늘어나면 < 연산과 ++ 연산의 수행횟수도 늘어나기 때문이다.
정리하면, 다른 연산들은 == 연산에 의존적이다.
따라서 == 연산의 횟수를 대상으로 시간 복잡도를 분석하면 된다.
이렇듯 알고리즘의 시간 복잡도를 계산하기 위해서는 핵심이 되는 연산이 무엇인지 잘 판단해야 한다. 그리고 그 연산을 중심으로 시간 복잡도를 계산해야 한다.
순차 탐색 알고리즘의 비교 연산횟수를 계산하는데... 순차 탐색 알고리즘은 운이 좋아서 찾고자 하는 값이 배열의 맨 앞에 저장되어 있으면 비교연산의 수행횟수는 1이 되고, 운이 없어서 찾고자 하는 값이 배열의 맨 마지막에 저장되어 있거나 찾고자 하는 값이 아예 저장되어 있지 않으면 비교연산의 수행횟수는 n이 된다.
이렇듯 모든 알고리즘에는 가장 행복한 경우와 가장 우울한 경우가 각각 존재하며, 이를 전문용어로 '최선의 경우(Best Case)' 그리고 '최악의 경우(Worst Case)' 라 한다.
그런데 알고리즘을 평가하는데 있어서 '최선의 경우'는 관심대상이 아니다. 어떠한 알고리즘이건 간에 최선의 경우는 대부분 만족할 만한 결과를 보이기 때문이다.
반면, 데이터의 수가 많아지면 '최악의 경우'에 수행하게 되는 연산의 횟수는 알고리즘 별로 큰 차이를 보인다. 따라서 알고리즘의 성능을 판단하는데 있어서 중요한 것은 '최악의 경우'이다.
평균적인 경우(Average Case) 는 시간 복잡도를 평가하는 정보로 의미를 지닌다. 하지만 문제는 이를 계산하는 것이 쉽지 않다는데 있다. 이를 계산하기 위해서는 다양한 이론이 적용되어야 하고, 분석에 필요한 여러 가지 시나리오와 데이터를 현실적이고 합리적으로 구성해야 하는데, 이는 쉽지 않은 일이다.
기본이 되는 다음 질문에 답을 하기조차 쉽지가 않다.
"무엇이 평균적인 상황인가?"
때문에 '평균적인 경우' 라고 주장하기 위해서는 다양한 자료들이 광범위하게 수집되어야 한다. 결국 일반적인 알고리즘의 평가에는 논란의 소지가 거의 없는 '최악의 경우(Worst Case)' 가 선택될 수 밖에 없다.
순차 탐색 알고리즘의 시간 복잡도 계산하기 : 최악의 경우(Worst Case)
계산할 것이 사실상 없다. 이 알고리즘의 흐름을 소스코드상에서 이해했다면, 다음 사실을 바로 파악할 수 있기 때문이다.
"데이터의 수가 n개일 때, 최악의 경우에 해당하는 연산횟수는(비교연산의 홧수는) n이다."
따라서 순차 탐색 알고리즘의 '데이터 수 n에 대한 연산홧수의 함수 T(n)'은 다음과 같다.
T(n) = n // 최악의 경우를 대상으로 정의한 함수 T(n)
이처럼 최악의 경우는 생각보다 쉽게, 코드의 분석을 통해서 구할 수 있는 경우도 많다.
순차 탐색 알고리즘의 시간 복잡도 : 평균적인 경우(Average Case)
평균적인 경우의 연산횟수 계산을 위해서 다음과 같이 두 가지를 가정한다.
1. 탐색 대상이 배열에 존재하지 않을 확률을 50%라고 가정한다.
2. 배열의 첫 요소부터 마지막 요소까지, 탐색 대상이 존재할 확률은 동일하다.
탐색 대상이 존재하지 않는 경우의 연산 횟수 n
탐색 대상이 존재하는 경우의 연산 횟수 n/2
그런데 탐색 대상이 배열에 존재하지 않는 경우와 존재하는 경우의 확률이 각각 50%이니 다음과 같이 이 둘을 하나의 식으로 묶어야 한다.
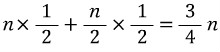
1/2씩 곱해서 더한 이유는 탐색 대상이 존재하지 않을 확률과 존재할 확률이 각각 50%이기 때문이다.
순차 탐색 알고리즘의 평균적인 경우의 시간 복잡도 함수: T(n) = 3/4n
※ 최악의 경우에 비해서 상대적으로 시간 복잡도를 구하는 것이 쉽지 않다는 사실에 주목해야 한다. 뿐만 아니라 평균적인 경우의 시간 복잡도 함수는 신뢰도가 높지 않다. 그 이유는 앞서 정의한 두 개의 가정을 뒷받침할 근거가 부족하기 때문이다.
프로그램의 성격에 따라서 그리고 데이터의 성격에 따라서 배열에 탐색 대상이 존재할 확률은 50%보다 높을 수도 있고 높지 않을 수 도 있는데 이러한 부분이 전혀 고려되지 않았다.
때문에 평균적인 경우의 시간 복잡도는 '최악의 경우'의 시간 복잡도보다 신뢰도가 낮다.
그래서 '최악의 경우'를 시간 복잡도의 기준으로 삼는 이유다!!!
'Programming > Data Structure' 카테고리의 다른 글
| 빅-오 표기법 (Big-Oh Notation) (5) | 2012.12.22 |
|---|---|
| 이진 탐색(Binary Search) 알고리즘 (0) | 2012.12.20 |
| 알고리즘의 성능분석 방법 (0) | 2012.12.20 |
| 자료구조와 알고리즘 (0) | 2012.12.19 |
| 자료구조(Data Structure)에 대한 기본적인 이해 (0) | 2012.11.15 |


